In its most basic form, the intersect test operation takes as input some object in an environment and some ray traversing that environment, and outputs whether the ray intersects the object, and if so, where. Furthermore, since the dominant method of representing an “object” in computer graphics is as a mesh of many flat polygons, the intersect test operation condenses to ray-triangle intersection testing.
While attractive in its simplicity, condensing intersect testing in ray tracing to iterated ray-triangle intersection is problematic vis-à-vis implementation performance. Let us say that we have an object composed of 10,000 polygons (in modern terms, this is a very modest size). And let us say that our ray tracing system is programmed to fire 1,000 rays. In this case, we have to perform 10,000 × 1,000 = 10,000,000 intersections. In general, the asymptotic complexity of a ray tracing system that fires R rays into an environment whose objects comprise n polygons is O(n) = Rn. Now, when one considers that systems that fire tens-of-thousands rays into environments of millions of polygons are common, then O(n) = Rn complexity becomes a performance handicap.
As a result, various acceleration techniques have been devised to improve ray tracing performance. Almost all such schemes work by transforming the asymptotic complexity of ray-object intersect testing from O(n) = Rn to O(n) = R log n for most objects. They work by progressively sub-dividing (or “partitioning”) the virtual 3D environment and the objects in it. Examples of such partitioning schemes include binary space partitioning trees and bounding volume hierarchies.
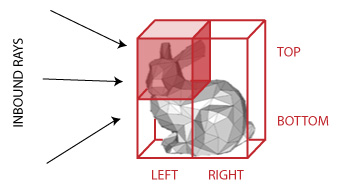
To see how acceleration works, consider the figure below. Here, several inbound rays are about to be intersect-tested against a 3D object (in this case, a low-complexity version of the classic Stanford Bunny). The triangular faces that comprise the surface mesh of the bunny are clearly visible. In a naïve ray tracer, each inbound ray would be intersect-tested against each polygon in the bunny, yielding a per-ray time complexity linear in the number of polygons.